题目：

802. 找到最终的安全状态

210. 课程表 II

5909. 并行课程 III

851. 喧闹和富有

剑指 Offer II 115. 重建序列

剑指 Offer II 114. 外星文字典

1.Kahn算法（卡恩算法）(BFS)

卡恩于1962年提出了该算法。简单来说，假设L是存放结果的列表，先找到那些「入度为零」的节点，把这些节点放到L中，因为这些节点没有任何的父节点。然后把与这些节点相连的边从图中去掉，再寻找图中的入度为零的节点。对于新找到的这些入度为零的节点来说，他们的父节点已经都在L中了，所以也可以放入L。重复上述操作，直到找不到入度为零的节点。如果此时L中的元素个数和节点总数相同，说明排序完成；

如果L中的元素个数和节点总数不同，说明原图中存在环，无法进行拓扑排序。

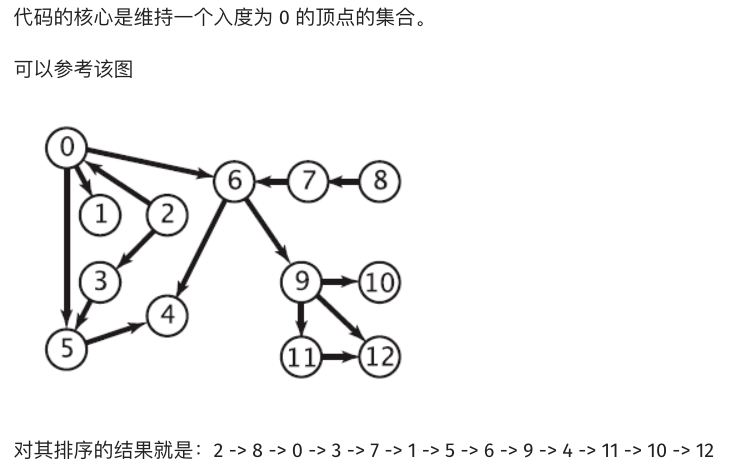
时间复杂度:$O(E+V)$，E表示边数，V表示节点数

伪代码

L ← 包含已排序的元素的列表，目前为空
S ← 入度为零的节点的集合
当 S 非空时：
    将节点n从S移走
    将n加到L尾部
    选出任意起点为n的边e = (n,m)，移除e。如m没有其它入边，则将m加入S。
    重复上一步。
如图中有剩余的边则：
    return error   (图中至少有一个环)
否则： 
    return L   (L为图的拓扑排序)

int N_Node = ; // 图中节点数量
// 建立邻接表, 保存当前点能到那些节点
List<List<Integer>> adj = new ArrayList<>(); 
int[] inEdge = new int[N_Node]; // 表示当前节点的入度
for (int i = 0; i < N_Node; ++i) {
    adj.add(new ArrayList<>());
}
for (int[] edge : prerequisites) {
    // 保存由节点出发所到达的点
    adj.get(edge[1]).add(edge[0]);
    // 所到达点的入度 + 1
    ++inEdge[edge[0]];
}
Queue<Integer> q = new LinkedList<>();
// 先将入度为0的节点加入队列
for (int i = 0; i < N_Node; ++i) {
    if (inEdge[i] == 0) {
        q.offer(i);
    }
}
List<Integer> ans = new ArrayList<>();
while (!q.isEmpty()) {
    int now = q.poll();
    ans.add(now);
    for (int v : adj.get(now)) {
        if (--inEdge[v] == 0) {
            q.offer(v);
        }
    }
}

// 如果ans.size() ≠ N_Node,表示图中有环，否则，ans为一个拓扑排序序列

2.DFS

深度优先搜索以任意顺序循环遍历图中的每个节点。若搜索进行中碰到之前已经遇到的节点，或碰到叶节点，则中止算法。

时间复杂度：$O(E+V)$

空间复杂度：$O(V)$

伪代码：

L ← 包含已排序的元素的列表，目前为空
当图中存在未永久标记的节点时：
    选出任何未永久标记的节点n
    visit(n)
    
function visit(节点 n)
    如n已有永久标记：
        return
    如n已有临时标记：
        stop   (不是定向无环图)
    将n临时标记
    选出以n为起点的边(n,m)，visit(m)
    重复上一步
    去掉n的临时标记
    将n永久标记
    将n加到L的起始

vector<int> G[MAXN];  // vector 实现的邻接表
int c[MAXN];          // 标志数组
vector<int> topo;     // 拓扑排序后的节点

bool dfs(int u) {
  c[u] = -1;
  for (int v : G[u]) {
    if (c[v] < 0)
      return false;
    else if (!c[v])
      if (!dfs(v)) return false;
  }
  c[u] = 1;
  topo.push_back(u);
  return true;
}

bool toposort() {
  topo.clear();
  memset(c, 0, sizeof(c));
  for (int u = 0; u < n; u++)
    if (!c[u])
      if (!dfs(u)) return false;
  reverse(topo.begin(), topo.end());
  return true;
}

参考资料

[1]https://oi-wiki.org/graph/topo/

[2]https://zh.wikipedia.org/wiki/%E6%8B%93%E6%92%B2%E6%8E%92%E5%BA%8F