跳表

本文最后更新于：2024年2月12日 晚上

跳表：SkipList

跳表是一种概率数据结构，用于有序集合的快速搜索查找，支持$O(logn)$时间复杂度的插入、查找、删除。在性能上与红黑树、AVL树相当，但是在实现上比这二者简单，redis中zset的实现使用了这种数据结构。

底层结构：链表（多级链表）

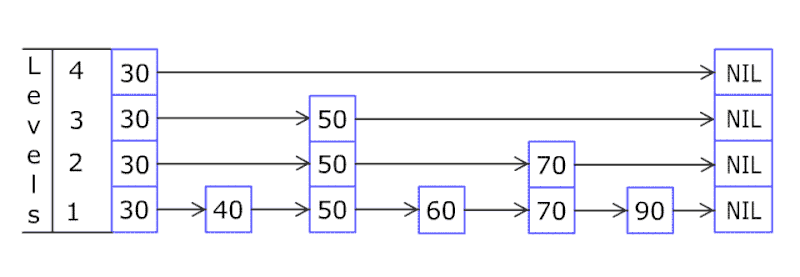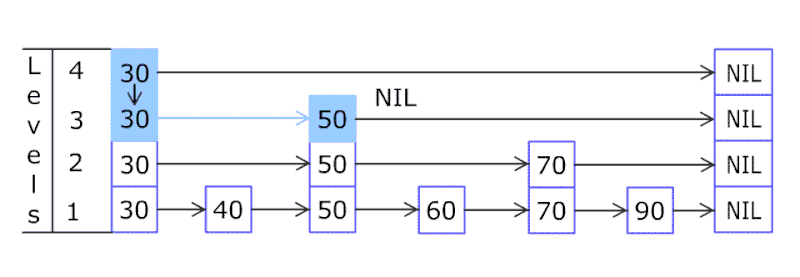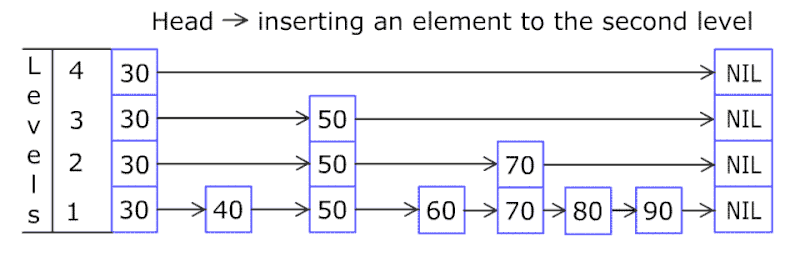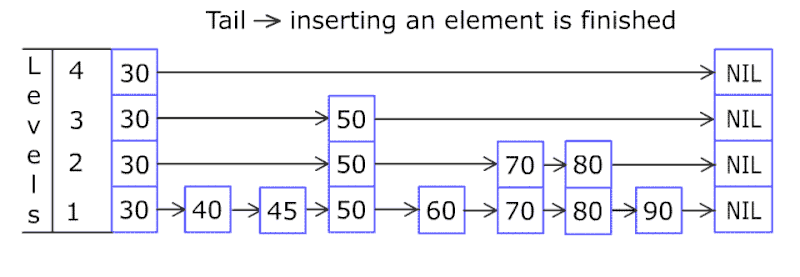
20220301160856

简单实现

1206. 设计跳表

Redis: zset源码

1.定义skiplist节点

class Node {
    int val; // 节点存储的值
    Node[] next; // 保存节点在对应层的下一个节点的指针
    
    public Node(int val, int level) {
        this.val = val;
        this.next = new Node[level]; // 表示当前节点有level层
    }
}

2.定义常量

// skiplist 头节点
private Node head;

// 当前跳表的最大层数
private int currentLevel = 1;

// skiplist的最大层数：可以满足2^64个元素的存储
private static final int SKIPLIST_MAX_LEVEL = 32;

// 节点是否进行层数增长的概率阈值
private static final double SKIPLIST_P = 0.25;

3.定义两个辅助函数

getRandomLevel

在新建节点时，通过“摇骰子”的方式确定新建节点的层数

private int getRandomLevel() {
    int level = 1;
   	// 只要“摇骰子”的结果大于阈值，并且level小于最大层数，就一直增大当前节点的层数
    while (Math.random() > SKIPLIST_P && level < SKIPLIST_MAX_LEVEL) {
        level++;
    }
    return level;
}
getClosestNode

找到在指定层idx中，于要查找值val最接近的节点

idx：指定的层id

val：要查找的值

private Node getClosestNode(Node node, int idx, int val) {
    while (node.next[idx] != null && val > node.next[idx].val) {
        node = node.next[idx];
    }
    return node;
}

4.insert：插入操作

允许插入重复值。插入时根据新建节点的层数，进行逐层插入。

public void insert(int val) {
    int level = getRandomLevel();
    Node temHead = head;
    Node node = new Node(val, level); // 要插入的新节点
    for (int i = currentLevel - 1; i >= 0; i--) {
        temHead = getClosestNode(temHead, i, val);
        // 当前层数小于新建节点的层数
        if (i < level) {
            if (temHead.next[i] == null) {
                // 该节点是尾节点，直接将新节点插到最后
                temHead.next[i] = node;
            } else {
                // 否则将新节点插到前后两个节点中间
                node.next[i] = temHead.next[i];
                temHead.next[i] = node;
            }
        }
    }
    // 如果新建节点的层数大于skiplist最大层数，那么直接在头节点对应层进行插入
    if (level > currentLevel) {
        for (int i = currentLevel; i < level; i++) {
            head.next[i] = node;
        }
        currentLevel = level;
    }
}

5.search：查找元素

// 查找是否存在值为val的节点
public boolean search(int val) {
    Node temHead = head;
    for (int i = currentLevel - 1; i >= 0; i--) {
        temHead = getClosestNode(temHead, i, val);
        if (temHead.next[i] != null && temHead.next[i].val == val) {
            return  true;
        }
    }
    return false;
}

6.deleteNode：删除节点

// 删除值为val的节点
public boolean deleteNode(int val) {
    boolean isDelete = false;
    Node temHead = head;
    // 逐层查找，逐层删除
    for (int i = currentLevel - 1; i >= 0; i--) {
        temHead = getClosestNode(temHead, i, val);
        if (temHead.next[i] != null && temHead.next[i].val == val) {
            // 链表删除节点
            temHead.next[i] = temHead.next[i].next[i];
            isDelete = true;
        }
    }
    return isDelete;
}

测试

SkipList skipList = new SkipList();
skipList.insert(1);
skipList.insert(2);
skipList.insert(3);
System.out.println(skipList.search(0)); // 应为false：还未插入0
skipList.insert(4);
System.out.println(skipList.search(1)); // 应为true
System.out.println(skipList.deleteNode(0)); // 应为false：没有0，无法删除
System.out.println(skipList.deleteNode(1)); // 应为true：成功删除节点1
System.out.println(skipList.search(1)); // 应为false：节点1已被删除

结果：

false
true
false
true
false

完整代码

public class SkipList {
	// skiplist 头节点
	private Node head;

	// 当前跳表的最大层数
	private int currentLevel = 1;

	// skiplist的最大层数：可以满足2^64个元素的存储
	private static final int SKIPLIST_MAX_LEVEL = 32;

	// 节点是否进行层数增长的概率阈值
	private static final double SKIPLIST_P = 0.25;

	public SkipList() {
		this.head = new Node(-1, SKIPLIST_MAX_LEVEL);
	}

	// 插入节点值为val的新节点
	public void insert(int val) {
		int level = getRandomLevel();
		Node temHead = head;
		Node node = new Node(val, level); // 要插入的新节点
		for (int i = currentLevel - 1; i >= 0; i--) {
			temHead = getClosestNode(temHead, i, val);
			// 当前层数小于新建节点的层数
			if (i < level) {
				if (temHead.next[i] == null) {
					// 该节点是尾节点，直接将新节点插到最后
					temHead.next[i] = node;
				} else {
					// 否则将新节点插到前后两个节点中间
					node.next[i] = temHead.next[i];
					temHead.next[i] = node;
				}
			}
		}
		// 如果新建节点的层数大于skiplist最大层数，那么直接在头节点对应层进行插入
		if (level > currentLevel) {
			for (int i = currentLevel; i < level; i++) {
				head.next[i] = node;
			}
			currentLevel = level;
		}
	}

	// 查找是否存在值为val的节点
	public boolean search(int val) {
		Node temHead = head;
		for (int i = currentLevel - 1; i >= 0; i--) {
			temHead = getClosestNode(temHead, i, val);
			if (temHead.next[i] != null && temHead.next[i].val == val) {
				return  true;
			}
		}
		return false;
	}

	// 删除值为val的节点
	public boolean deleteNode(int val) {
		boolean isDelete = false;
		Node temHead = head;
		// 逐层查找，逐层删除
		for (int i = currentLevel - 1; i >= 0; i--) {
			temHead = getClosestNode(temHead, i, val);
			if (temHead.next[i] != null && temHead.next[i].val == val) {
				// 链表删除节点
				temHead.next[i] = temHead.next[i].next[i];
				isDelete = true;
			}
		}
		return isDelete;
	}

	// 在新建节点时，通过“摇骰子”的方式确定新建节点的层数
	private int getRandomLevel() {
		int level = 1;
		// 只要“摇骰子”的结果大于阈值，并且level小于最大层数，就一直增大当前节点的层数
		while (Math.random() > SKIPLIST_P && level < SKIPLIST_MAX_LEVEL) {
			level++;
		}
		return level;
	}

	// 找到在指定层idx中，于要查找值val最接近的节点
	private Node getClosestNode(Node node, int idx, int val) {
		while (node.next[idx] != null && val > node.next[idx].val) {
			node = node.next[idx];
		}
		return node;
	}


	class Node {
		int val; // 节点存储的值
		Node[] next; // 保存节点在对应层的下一个节点的指针

		public Node(int val, int level) {
			this.val = val;
			this.next = new Node[level]; // 表示当前节点有level层
		}
	}
}

参考

http://zhangtielei.com/posts/blog-redis-skiplist.html

https://fankeke.github.io/2019/10/01/%E6%B7%B1%E5%85%A5%E7%90%86%E8%A7%A3redis%E4%B8%AD%E7%9A%84zset%E5%AF%B9%E8%B1%A1/