二进制操作

序号	操作	代码
1	计算 i 对于其子集 j 的 补集	i ^ j
2	判断 i 是否为 j 的 子集	( i \	j ) == j
3	i 去掉指定位置的 1	( i & (~( 1 << n ) ) )
4	判断 i 和 j 是否有交集	(i & j) == 0
5	移除二进制表示中最右侧的1 Brian Kernighan 算法：$f(x)=x \& (x-1)$	x = x & (x - 1)
6	异或运算^可以理解成是不带进位的加法

题目：
473. 火柴拼正方形

二进制枚举

常用在求不同的组合的问题中，如：7 选 5 的所有组合，求集合的所有子集

原理：利用数字的「二进制表示」中 1 的位置和个数的不同来确定所有组合。

例如：集合大小为7，则其所有子集共有128个（包括空集），0～128的每一数字的二进制表示代表每种子集，0代表不选该位置的元素，1表示选择。

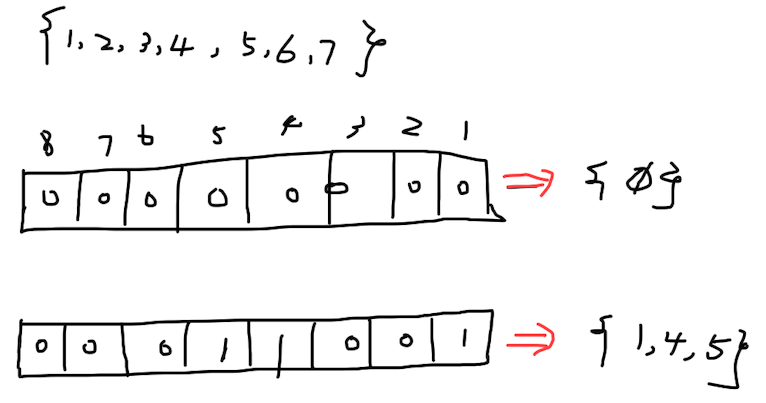
// 以求大小为7的集合的子集为例
for (int i = 0; i < 1<<7; i++) { // 1<<7 = 128 = 2 ^ 7
    for (int j = 0; j < 7; j++) {
        if ((i >> j) & 1 == 1) { // 表示选该位置的元素
            System.out.print(nums[j] + " ");
        }
    }
    System.out.println();
}

枚举二进制子集

// 枚举二进制子集
for (int i = 1; i <= 5; i++) {
    // 枚举出i的所有二进制子集
    for (int j = i; j > 0; j = (j - 1) & i) {
        System.out.print(j + " ");
    }
    System.out.println();
}

输出：

1 (01)
2 (10)
3 2 1 (11, 10, 01)
4 (100)
5 4 1 (101, 100, 001)