前缀和

前缀和可以在$O(1)$时间内的计算一块区域的总和

一维前缀和

3127. 来，骗

// 计算 
int[] getPrefix(int[] arr) {
    int n = arr.length;
    int[] prefix = new int[n+1]; // 添加一位初始和，简化代码
    for (int i = 1; i <= n; i++) {
        prefix[i] = prefix[i-1] + arr[i-1];
    }
    return prefix;
}

// 查询
int getSum(int[] prefix, int l, int r) {
    return prefix[r] - prefix[l-1];
}

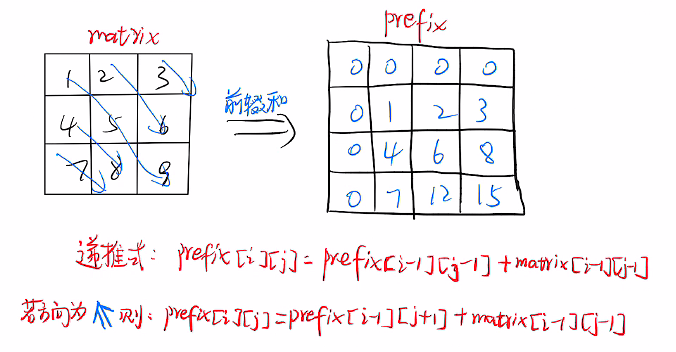
一维前缀和拓展：斜着的一维前缀和

力扣 1878. 矩阵中最大的三个菱形和

原理和普通一维前缀和一样，但是需要找到对应方向上所有点坐标的递推公式：

// 构建
int n = matrix.length, n = matrix[0].length;
int[][] prefix1 = new int[n+2][m+2]; // 左上---右下
int[][] prefix2 = new int[n+2][m+2]; // 右上---左下
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
        prefix1[i][j] = prefix[i-1][j-1] + matrix[i-1][j-1];
        prefix2[i][j] = prefix[i-1][j+1] + matrix[i-1][j-1];
    }
}

// 查询 : (x2, y2) --- (x1, y1)
sum = prefix[x2][y2] - prefix[x1-1][y1-1];

二维前缀和

1314. 矩阵区域和

304. 二维区域和检索 - 矩阵不可变

// 计算
// prefix[i][j]表示从（0，0）到（i，j）这一矩形和总和
int[][] getPrefix(int[][] matrix) {
    int n = matrix.length, m = matrix[0].length;
    int[][] prefix = new int[n+1][m+1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            prefix[i][j] = prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1] + matrix[i-1][j-1];
        }
    }
    return prefix;
}

$$S_{1} = prefix[1][1] = prefix[x_{1}-1][y_{1}-1] \\ S_{2} = prefix[1][3] - S_{1} = prefix[x_{1}-1][y_{2}] - prefix[x_{1}-1][y_{1}-1] \\ S_{3} = prefix[3][1] - S_{1} = prefix[x_{2}][y_{1}-1] - prefix[x_{1}-1][y_{1}-1] \\ sum = prefix[3][3] - S_{1} - S_{2} - S_{3} \\ =prefix[x_{2}][y_{2}] + prefix[x_{1} -1][y_{1}-1] - prefix[x_{1}-1][y2] - prefix[x_{2}][y_{1}-1]$$

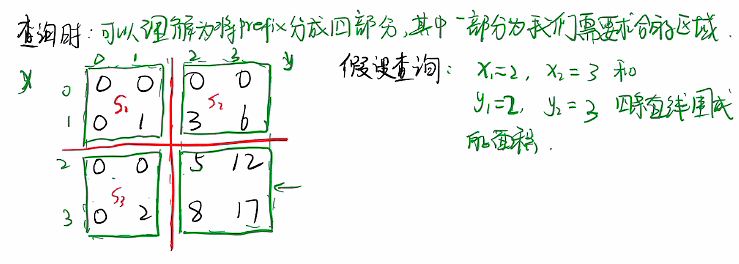
//查询
int getSum(int[][] prefix, int x1, int y1, int x2, int y2) {
    return prefix[x2][y2] + prefix[x1-1][y1-1] - prefix[x1-1][y2] - prefix[x2][y1-1];
}

二维前缀和特殊用法：计算元素出现的个数

前缀和数组$prefix[r][j] - prefix[l][j]$表示在区间$（l，r）$中 元素$j$出现的次数。

例如：对于数组 nums = [4, 5, 2, 2, 7, 10]$（1 \le nums[i] \le 100）$, 要求快速查询指定下标区间$l-r$之间每一个元素出现的个数。

可通过构造前缀和来实现快速的查询。

int n = nums.length;
int[][] prefix = new int[n+1][101]; // 101表示数据范围，可根据题意修改
// 构造前缀和
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= 100; j++) {
        int t = 0; // 表示当前数是否在数组中出现
        if (nums[i-1] == j) t = 1; // 出现该数
        prefix[i][j] = prefix[i-1][j] + t; // 前缀和更新
    }
}

// 查询 : 下标 1 ～ 5  之间 2 出现的个数
int res = prefix[5+1][2] - prefix[1][2];

相关题目：1906. 查询差绝对值的最小值

class Solution {
    public int[] minDifference(int[] nums, int[][] queries) {
        int n = nums.length, m = queries.length;
        List<Integer> ans = new ArrayList<>();
        int[][] prefix = new int[n+1][101]; // l~r 之间 1～100出现的个数
        // 计算前缀和
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= 100; j++) {
                int t = 0;
                if (nums[i-1] == j) { // 当前数出现
                    t = 1;
                }
                prefix[i][j] = prefix[i-1][j] + t;
            }
        }

        for (int i = 0; i < m; i++) {
            int l = queries[i][0], r = queries[i][1];
            int last = 0, best = Integer.MAX_VALUE;
            // 枚举计算查询中的最小值
            for (int j = 1; j <= 100; j++) {
                if (prefix[r+1][j] - prefix[l][j] > 0) {
                    if (last > 0) // 只有至少出现一个数才更新答案
                        best = Math.min(best, j - last);
                    last = j; // 更新为上一个出现的数
                }     
            }
            if (best != Integer.MAX_VALUE) ans.add(best);
            else ans.add(-1); // 所有元素都相同的情况
        }

        int[] res = new int[ans.size()];
        for (int i = 0; i < ans.size(); i++) res[i] = ans.get(i);
        return res;
    }
}

时间复杂度：计算前缀和：$O(nC)$，查询答案:$O(qC)$，其中$n$和$q$分别是$nums$和$queries$的长度，$C$是$nums$中的最大值。总时间复杂度为：$O((n+q)C)$.

空间复杂度：$O(nC)$，为存储前缀和的空间。

差分

可以用来在$O(1)$时间内计算给一块区域的所有位置都加上或者减去一个数。

主要可以分为两步：1.构建差分数组。2.进行完操作后还原

一维差分

797.差分

3617. 子矩形计数

离散化差分：针对区间范围很大的情况

732. 我的日程安排表 III

核心公式：

1.计算

$diff[0] = arr[0]$

$diff[i] = arr[i] - arr[i-1] (i>0)$

2.还原

$diff[0] = diff[0]$

$diff[i] = diff[i]-diffi-1$

例子🌰：

$diff[0] = arr[0]$

$diff[1] = arr[1] - arr[0]$

$diff[2] = arr[2] - arr[1]$

$diff[3] = arr[3] - arr[2]$

给下标（1，2）内的所有点都加上常数c

$diff[1] = diff[1] + c = arr[1] - arr[0] + c$

$diff[3] = diff[3] - c = arr[3] - arr[2] - c$

还原：

$diff[1] = diff[1] + diff[0] = arr[1] - arr[0] + c - arr[0] = arr[1] + c$

$diff[2] = diff[2] + diff[1] = arr[2] - arr[1] + arr[1] + c = arr[2] + c$

$diff[3] = diff[3] + diff[2] = arr[3] - arr[2] - c + arr[2] + c = arr[3]$

// 1.构建差分数组
int n = arr.length;
int[] diff = new int[n+1]; // 多一位保存diff[n]
for (int i = 0; i < n; i++) {
    diff[i] += arr[i];
    diff[i+1] -= arr[i];
}

// 操作：如，为在下标（2， 5）之间的所有数都加上 c
diff[2] += c;
diff[5+1] -= c;

// 2.还原
for (int i = 1; i < n; i++) {
    diff[i] += diff[i-1];
}

二维差分

5931. 用邮票贴满网格图

1.构建

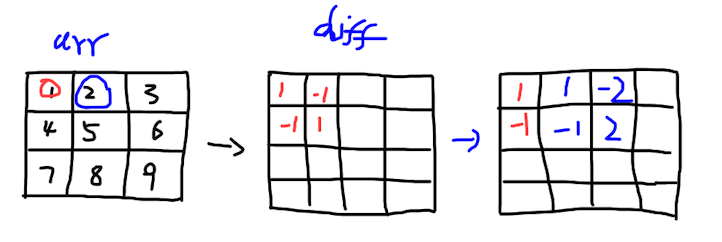
// 构建
int n = arr.length, m = arr[0].length;
int[][] diff = new int[n+2][m+2]; // 加两维是为了简化边界和防止越界
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        int t = arr[i-1][j-1];
        diff[i][j] += t;
        diff[i + 1][j + 1] += t;
        diff[i][j + 1] -= t;
        diff[i + 1][j] -= t;
    }
}

2.操作：为点（x1, y1) , (x2, y2)确定的矩形中的所有点都加上常数c

// 操作
diff[x1][y1] += c;
diff[x2][y2] += c;
diff[x1][y2+1] -= c;
diff[x2+1][y1] -= c;

3.还原

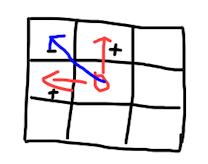
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
        diff[i][j] += diff[i-1][j] + diff[i][j-1] - diff[i-1][j-1];
    }
}